Bonsoir
c'est peu être un peu technique , mais il en faut pour tous, les amateurs de méthodes et de modèles y trouveront leur compte. Pour les autres, il vous suffit de lire les 3 dernières ligne
C'est un excercice fait avec un ami lors de la semaine dernière dans aucun cadre particulier , avant tout histoire de nous faire notre propre idée sur ce prochain hiver. Nous n'avons pas les outils ni les données des professionnels, mais on peut quand même faire des choses convainquantes
Notre bu était de faire un test pour voir si ce début d'hiver a des chances de depasser les normales climatiques ou non pour les températures
après chancun pense ce qu'il veut
Bonjour et bienvenue sur ce bulletin complet de ce début de journée du 3 décembre, rédigé pour le Massif Central et les Alpes pour les 10 prochains jours
Notre Objectif
Notre étude vise à modéliser et à prévoir la probabilité de dépassement de la température normale climatique sur un site. Nous disposons pour cela de données météorologiques de la station de Lyon Bron Ce travail comprend deux volets. Le premier a consisté en la sélection des variables les plus significatives pour la prévision de cette probabilité. Cette opération a été réalisée avec le modèle utilisé pour la prévision : les chaînes de Markov cachées multidimensionnelles (CMC-MD). Quatre variables ont été retenues sur un total de seize, elles semblent de plus présenter une bonne cohérence avec le phénomène d’un point de vue météorologique. Le second volet a été la prévision, reposant aussi sur des CMC-MD. Un plan d’expérience a permis de dresser le profil de l’évolution moyenne du résultat en fonction des variations des paramètres d’entrée, assez nombreux à régler, afin d’automatiser l’ensemble. On aboutit donc à un système qui offre de bonnes performances dans le cadre d’une prévision à 1 ou 2 mois.
La méthode
Les chaînes de Markov cachées sont des outils de modélisation très utilisés dans de nombreux domaines, en reconnaissance des formes plus particulièrement .Ce modèle est formé de deux composantes : les observations, mesurées a priori et les états, cachés, inobservables, estimé a posteriori. A chaque état caché d'une CMC est associé une distribution de probabilités d'émission de symboles. A partir d'une suite observée de tels symboles il est possible d'estimer, au cours d’une étape d’apprentissage, les paramètres d'une CMC. Ce modèle résultat reconnaît alors la suite apprise dans le sens où la succession d’états cachés correspondante est plus probable que les autres. Le nombre de "degrés de liberté" (paramètres) important de ce type de processus stochastique est un facteur prépondérant pour justifier l'emploi des CMC pour la modélisation de processus stochastiques complexes tels que la reconnaissance de la parole, la modélisation du langage, la reconnaissance de caractères manuscrits, le traitement du signal ou l'analyse des images. Une limitation de ces outils est la prise en compte que d’une seule variable observable. Dans le cas où le processus peut être caractérisé au cours du temps par plusieurs variables, on est obligé de procéder à un recodage dans l’espace des combinaisons de ces variables. On cherche alors à discrétiser assez fortement chacune des variables afin que l’espace des combinaisons ne soit pas trop grand, ce qui mènerait à un apprentissage difficile. Une solution alternative est l’emploi de chaînes de Markov cachées multidimensionnelles Ce type de modèle permet de modéliser plusieurs processus observables simultanément sous l’hypothèse qu’il n’existe qu’un seul processus caché sous jacent.
La durée
Le modèle fonctionne à partir des écarts à la normale quotidiens de 10 paramètres météorologiques, des valeurs quotidiennes (et/ ou horaire ) brutes de la même station, ainsi que de 12 variables illustratives telle que la NOA, la variation de pression quotidienne etc…… L’ensemble des hivers 12 dernières années.
Le Tableau constitué est formé de 32 colonnes et de 6380 individus (matrice quotidienne ). Ce qui représente un tout petit tableau pour un modèle, c’est donc un faible échantillon.
Etude des variables : faible influence de la NOA
Avant de caractériser d’établir la modélisation. Pour chaque variable continue caractérisante, on calcule la statistique de Fisher associée à l’analyse de la variance où la variable continue est la variable à expliquer et la variable nominale à décrire est le facteur. Pour chacune de ces statistiques de Fisher, on calcule la probabilité associée. La valeur test est la valeur de la loi normale centrée réduite qui a la même probabilité d’être dépassée. L’analyse de la variance où la variable continue est « la mieux prévisible » à l’aide du facteur correspondant à celle où la statistique de Fisher est la plus significative.
Ici la température moyenne journalière est la variable à caractériser. Et on remarque que sa corrélation avec l’indice de la NOA est seulement de 0.25 ou 1 est le maximum. La NOA arrive seulement en 8ème position. On peut donc mettre en doute comme l’ont fais déjà de nombreux experts l’influence de la NOA sur la variabilité des températures de ces 10 dernières années.
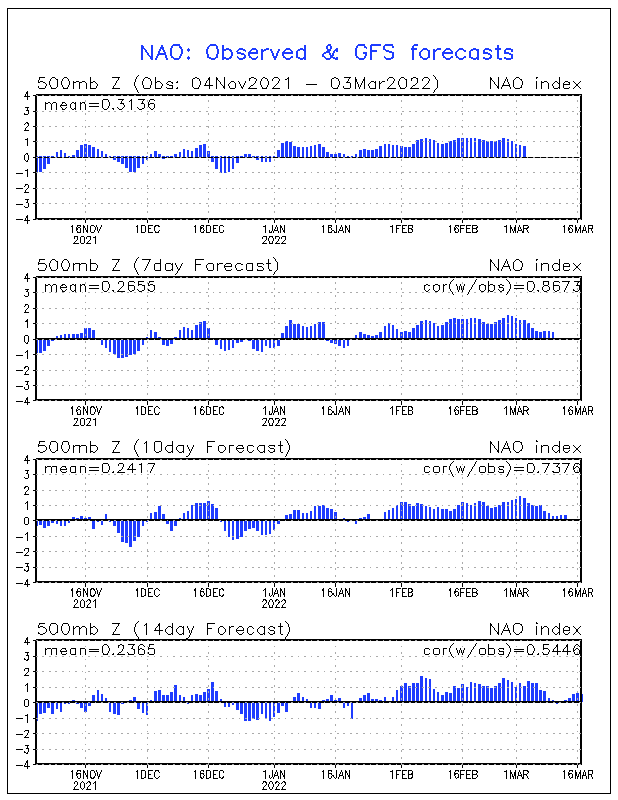
Le flux à 500 hPa, mesuré sur 360° est la variable la plus caractérisante.
Apprentissage du modèle
Aussitôt la construction d’un modèle effectuée, on cherche à avoir un indicateur de la
pertinence de l’apprentissage. Classiquement on a deux méthodes à notre disposition. La première repose sur l’algorithme Forward et la seconde sur l’algorithme de Viterbi. Cet indicateur va nous servir ici à déterminer la corrélation qu’il y a entre les variables. Le principe est de modéliser une variable et de tester la qualité de
l’apprentissage avec une seconde. Si l’indicateur est élevé, le processus caché modélisé est bien adapté également à la variable qui n’a pas servi à la construction du modèle. D’un point de vue modélisation, cela signifie que les changements de lois de probabilités des symboles observés se font sensiblement aux mêmes instants. Les différents indicateurs attestent une modélisation robuste ou seulement 2 variables sont écartées (Humidité et Ultraviolet)
La prévision
Le système de prévision sur cette ligne d’algorithme est plus délicate et montre une limite au-delà de 1.5 mois en raison du faible tableau de valeur
En conclusion directe, la probabilité selon ce modèle et ces variables de départ de dépasser la normale climatique 1971- 2000 pour ce mois de décembre est de 72%, avec un dépassement moyen de 0.8°, pour les deux premières décades de janvier elle est de 68% avec un écart moyen de 0.6°
référence surun autre excercice du même genre
tbrouard.univ-tours.fr













inscrit le 19/12/05
3444 messages